저희는 지난 글에서 델타헷지가 어떻게 작동하는지에 대해 이론적인 부분을 살펴보았습니다. 그럼 이번에는 실제로 구현된 결과를 보면서 델타헤지의 함의를 알아보겠습니다. 이번 주제의 궁극적인 목표는 모델을 이용해 계산한 Greeks가 실제 실현된 옵션 변동을 얼마나 설명하는지 확인하는 것입니다. 따라서 이 목표를 달성하기 위해 가장 간단한 BSM 으로 출발하여 점점 가정을 완화시켜 실제 데이터로 적용시켜보도록 하겠습니다.
우선 이번 글에서는 BSM의 손익이 어떻게 발생하는지 구현된 코드로 확인하고, 또 실제 Greeks가 손익을 얼마나 설명하는지 살펴보겠습니다.
우선 BSM model하에서 이론적으로 델타 헷지를 한다는 것은 무슨 뜻인지 알아보겠습니다. BSM PDE는 주가가 GBM을 따르며 파생상품이 $S,t$에만 의존하는 함수일 때 만족합니다. 따라서 BSM으로 델타헷지를 했을 때 얻은 함의를 관찰하기 위해서는 주가를 GBM으로 생성해야 합니다. 만약 실제로 주가가 GBM을 따를 경우, 델타헤지만으로 헤지 PnL이 0이된다는 것을 지난 글에서 확인했습니다. 그러나 현실에서는 이산헷지만 가능하므로, 헷지 PnL은 확률 1로 0이 되는 것이 아니라 평균이 0인 확률적 분포를 갖고, 이때 분산이 헷지 주기에 비례한다는 것을 이론적으로 도출했습니다. 실제로 시뮬레이션 결과 헷지 주기에 따른 헷지 성과 분포는 다음과 같이 나타났습니다.
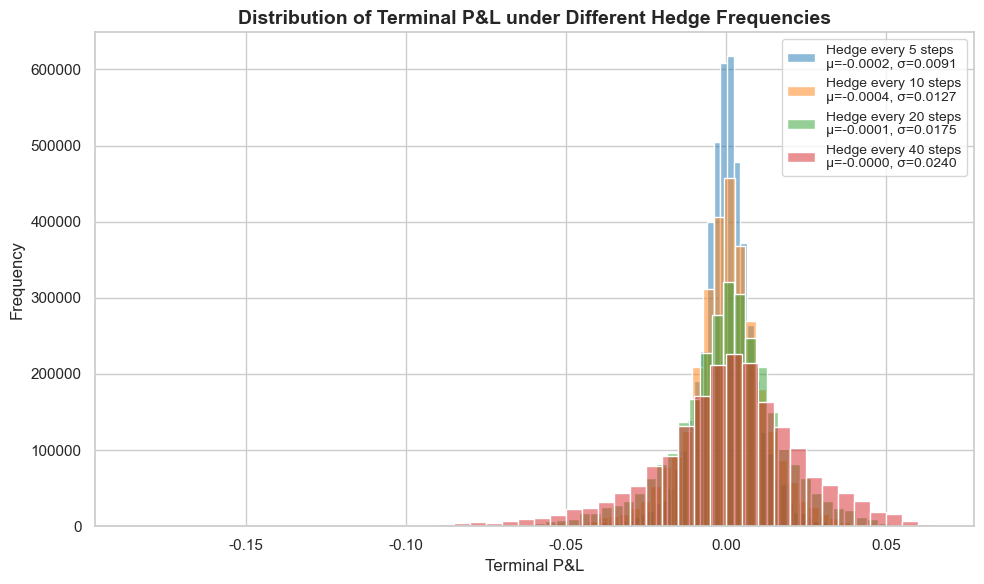
한편 지난 글에서 살펴봤듯이 Hedge pnl은 다음과 같이 정의할 수 있었습니다.
$$P\&L = -\left[ P(t + \delta t, S + \delta S) - P(t, S) \right] + r P(t, S) \, \delta t + \Delta \left( \delta S - r S \delta t + q S \delta t \right)$$
중요한 점은, 이 식을 이용하여 헷지 PnL을 구하기 위해서는 파생상품의 가격 $P(t + \delta t, S + \delta S)$가 주어져야 합니다. 이때 이 가격이 model 가격인지, 실제 가격인지에 따라 실제 PnL이 달라지며 이 점이 앞으로 저희가 관찰해야할 주된 차이점입니다.
만약 파생상품 가격이 모델 가격과 일치한다면 약간의 식 변형을 통해 Cash gamma의 형태로도 나타낼 수 있었습니다.
$$P\&L = -\frac{S^2}{2} \cdot \frac{d^2 P_{\hat{\sigma}}}{dS^2} \left( \frac{(\delta S)^2}{S^2} - \hat{\sigma}^2 \delta t \right)$$
실제로 두 손익 PnL은 거의 유사하게 나오는 것을 확인할 수 있습니다.

이제 델타 헤지의 매커니즘에 대해 좀더 살펴보겠습니다. 블랙 숄즈 모델에 따르면 손익은 delta, gamma, theta로 설명되어야 합니다. 여기서 vega는 블랙 숄즈 PDE에서 나타나지 않으므로 우선은 고려하지 않겠습니다.(실제로 Vega라는 그릭스 문자는 존재하지 않습니다.)
그럼 실제로 두 개의 path를 비교해가며 실제 손익이 greeks로 잘 분해되는지 살펴보겠습니다. 이것이 중요한 이유는 우리가 모델을 설정하고 만약 시장이 모델과 유사하게 움직인다면 현재 시점에서 계산한 Greeks를 이용하여 다음 시점 market factor(시간, 기초자산, 변동성)가 움직였을 때 나의 포지션 변화를 예측할 수 있기 때문입니다. 그렇게 할 수 있어야 트레이더는 오늘 그릭스를 보고 내일 예상되는 시장의 변화를 대응할 수 있으므로 굉장히 중요합니다. 따라서 1) 현실과 잘 맞는 모델을 설정하고 2) 정확히 greeks를 계산하여 정합성이 높은 시스템을 구축하는 것이 파생상품 운용에 있어 중요합니다.

path 1은 주가가 만기에 행사가 아래로 빠져 옵션이 otm으로 가는 경우이고 path2는 itm으로 가는 경우입니다. 이 때 실제 pnl과 greeks로 설명되는 pnl은 다음과 같이 나타납니다.

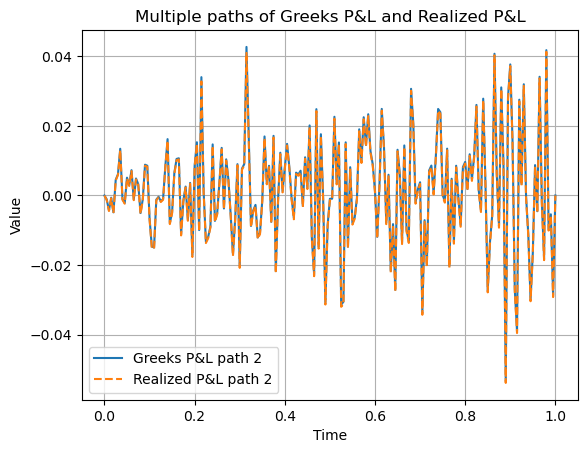
얼핏 봤을때는 Greeks로 예측한 큰 차이가 없어보입니다. 실제로 그럴까요? 만약 주가가 모델대로 움직이고, 연속 헷지가 가능하다면 이는 일치해야합니다. 왜냐하면 실제 PnL에서 옵션 가치는 연속헷지와 GBM가정에서 얻어진 analytic한 가격이기 때문이죠. 그러나 우리는 주가를 모델대로 시뮬레이션 할 수 없고(GBM을 이산화) 연속 헷지도 불가능하므로 둘 사이의 오차가 발생하게 됩니다. 그럼 오차의 크기는 어떻게 결정할까요? 테일러 전개를 떠올려 보면 기초자산의 변화가 큰 경우 Gamma보정으로는 설명이 안되는 High order term이 커지게 됩니다. 따라서 우리는 기초자산의 변화가 직전보다 큰 경우 실제 PnL과 Greeks PnL의 차이가 클 것이라고 예상할 수 있습니다. 실제 그런지 확인해보겠습니다.
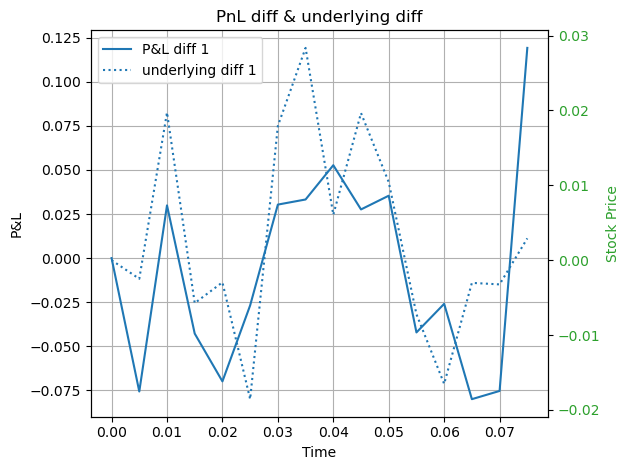

기초자산 변화에 따라 실제 PnL과 Greeks PnL의 차이가 관련이 있는 것처럼 보입니다. 따라서 이러한 근사는 market risk factor가 조금 변할때는 잘 맞을 수 있지만, 급변하는 시장상황에서는 예상과 다를 수 있으므로 포지션을 이해하기 위해서는 극단적 상황에 대한 추가적인 시나리오 분석이 이루어져야 합니다.
이번에는 손익에서 각각의 Greeks가 차지하는 비율을 알아보겠습니다. 수익이 양수일때와 음수일때 각각의 민감도의 기여도(%)는 다음과 같습니다.
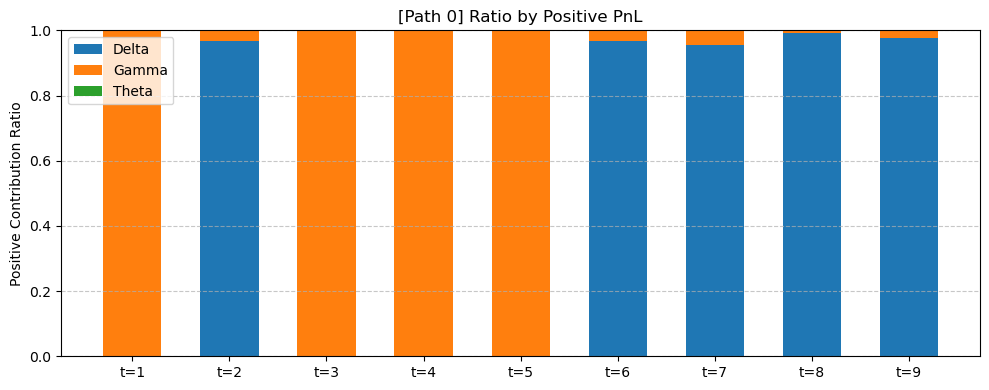

처음 관찰되는 것은 수익과 손실 대부분은 delta에 의해 결정되는 것을 확인할 수 있습니다. 따라서 파생상품을 안정적으로 운용하기 위해서는 delta를 막는것이 필연적입니다. 다음으로, Gamma는 양수인 손익에만 기여하며 Theta는 음수인 손익에만 기여하는 것을 알 수 있습니다. 이는 시장 변동이 '공정한' 양보다 더 많이 움직이는 경우 Gamma 손익이, 그렇지 않은 경우 Theta손실이 발생합니다.
지금까지 우리는 BSM가정이 잘 만족되었을 때 Delta hedge의 손익이 어떻게 나는지, 그리고 파생상품의 손익 분해가 어떻게 되는지 살펴보았습니다. 다음 글에서는 BSM model 가정을 조금 깨어 parameter로 사용되는 변동성이 중간에 달라지는 경우 손익의 pnl이 어떻게 나타나는지 살펴보겠습니다. 이후 BSM model이 아닌 Stochastic vol model에서의 손익을 분석해보고 최종적으로 실제 데이터를 이용하여 PnL 분해를 해보도록 하겠습니다.
'Quant > Equity' 카테고리의 다른 글
| 2차원 FDM(ADI,OSM) (0) | 2025.06.05 |
|---|---|
| PSOR 방법을 이용한 American option 가격 평가 (1) | 2025.06.05 |
| Local vol model(2) (0) | 2025.06.03 |
| Local vol model(1) (0) | 2025.06.03 |
| 변동성 곡면 (0) | 2025.06.02 |



댓글